Цикл лекций
«Фантастическая теория фантастики»:
Многомерное пространство
и парадоксы времени
Fr. Nyarlathotep Otis, 10.12.20141
 Fr. Nyarlathotep Otis: Давно планировал запустить курс, который называется «Фантастические теория фантастики». Название придумал Роберт Шекли, исходя из своего тезиса «фантастика должна быть реалистичной». Сейчас мы будем говорить о параллельных мирах и о парадоксах времени, но не с научной точки зрения (совсем не важно, насколько всё это действительно так, и есть ли эти параллельные миры): это именно попытка создать непротиворечивую концепцию, связанную с фантастическими сюжетами, — как и любая тема из «Фантастической теории фантастики». Этим подходом очень часто пренебрегают, и получается ерунда, когда, скажем, в фэнтезийном мире получаются противоречия банально по пластике тела во время боя, в космической фантастике — какие-то биологические или психологические нестыковки по инопланетным расам и т. п. К парадоксам времени мы будем подходить с той позиции, что время — это четвёртое измерение пространства. Это может быть так, может быть не так, кое-где мы будем пытаться заходить с других сторон, но в основном будем разрабатывать именно эту модель. Кстати, пикантная деталь: эта лекция основана на «сказках», которые я рассказываю на ночь моей дочке 🙂
Fr. Nyarlathotep Otis: Давно планировал запустить курс, который называется «Фантастические теория фантастики». Название придумал Роберт Шекли, исходя из своего тезиса «фантастика должна быть реалистичной». Сейчас мы будем говорить о параллельных мирах и о парадоксах времени, но не с научной точки зрения (совсем не важно, насколько всё это действительно так, и есть ли эти параллельные миры): это именно попытка создать непротиворечивую концепцию, связанную с фантастическими сюжетами, — как и любая тема из «Фантастической теории фантастики». Этим подходом очень часто пренебрегают, и получается ерунда, когда, скажем, в фэнтезийном мире получаются противоречия банально по пластике тела во время боя, в космической фантастике — какие-то биологические или психологические нестыковки по инопланетным расам и т. п. К парадоксам времени мы будем подходить с той позиции, что время — это четвёртое измерение пространства. Это может быть так, может быть не так, кое-где мы будем пытаться заходить с других сторон, но в основном будем разрабатывать именно эту модель. Кстати, пикантная деталь: эта лекция основана на «сказках», которые я рассказываю на ночь моей дочке 🙂
Итак, измерения. Нулевое измерение условно изображается вот так:
.
На самом деле оно не выглядит никак: с какой стороны мы ни смотрим, оно нулевого размера. Геометрию вы помните: через две точки можно провести единственную прямую. Но все эти аксиомы — что через две точки можно провести единственную прямую, что через три точки или две пересекающиеся прямые можно провести единственную плоскость, — всё это частные случаи одной аксиомы, которую лет 20 назад я сформулировал примерно так:
Через любые (n – m – l + 3) l-ориентированных m-измерений, не лежащих в одном (n – 1)-измерении, можно провести n-измерение, и притом только одно.
Здесь k = n – m – l + 3 определено как количество исходных измерений, l — как тип их взаимной ориентации (сейчас плохо помню, что к чему, и какая величина чему соответствовала, но это о понятиях вроде идентичности, параллельности, пересекаемости и скрещиваемости), m — исходная мерность, n — мерность, которую мы строим, а p = n – 1 — это измерение, в котором мы взаиморасполагаем исходные измерения (на одном из черновиков, наоборот, конечная мерность записывалась как p = n + 1, а пространство взаиморасположения — как n, что создаёт дополнительную путаницу, поскольку я не помню, какой из черновиков более поздний). Иначе говоря, для выстраивания конкретного пространства нам надо знать, какие пространства мы используем и как мы их взаимоориентируем. Звучит громоздко и непонятно, я не буду сейчас всё пересчитывать и перепроверять, но эти старые расчёты и наброски у меня сохранились, и на тех измерениях, которые мы можем «пощупать», всё хорошо подтверждалось, хотя где-то я и не помню логику подсчётов. В общем, как следствие получается, что через две точки, не идентичные друг другу, мы строим единственную прямую, через три, не лежащие на одной прямой — плоскость, через четыре, не лежащие в одной плоскости — трёхмерное пространство, через пять, не лежащих в одном трёхмерном пространстве (это нам уже представить сложнее) — четырёхмерное пространство и т. д. То же касается прямых: через две пересекающиеся мы строим плоскость, через три пересекающиеся, но не лежащие в одной плоскости, или через две скрещивающиеся — трёхмерное пространство и т. д. Две пересекающиеся плоскости дают трёхмерное пространство, две скрещивающиеся (тоже трудно представить, потому что скрещиваться в трёхмерном пространстве плоскости не могут) — четырёхмерное, как и два пересекающихся трёхмерных пространства и т. д.
Прямая — это первое измерение. Его мы тоже фактически видеть не можем, потому что для зрения нам нужна плоскость. Мы трёхмерные, но для зрения нам нужна плоскость. Однако мы можем представить её, и — сейчас начинается не столько геометрия, сколько фантастика — теоретически мы можем даже представить одномерное существо. Одномерное существо — это, фактически, отрезок. Отрезки эти могут ползать, но переползти один через другой они не могут. Они встретились — они разошлись. Это всё пространство их жизни. Они могут быть разных размеров, но всё равно они только встречаются и расходятся. А проекцией первого измерения на нулевое измерение будет нулевое измерение: проекция линии, проходящей через точку, идентична самому ноль-мерному пространству.
Далее. Если мы начинаем эту прямую линию загибать, то для его обитателей пространство останется одномерным, но для нас это уже выход на плоскость, потому что произвольно взятые точки не находятся на одной прямой. То же самое, что касается искривления нашего трёхмерного мира, о котором говорят космологи. Для нас это длина, высота, ширина, а если бы на наш мир смотрел кто-то четырёхмерный, он увидел бы у нас подобный же изгиб. Но об этом чуть позже.
Искривление — это один из вариантов выхода на плоскость. Второй вариант выхода на плоскость (и единственный выход на линию, поскольку «изогнуть» точку невозможно): мы можем выстроить в ряд параллельные прямые или сделать «сеточку» из пересекающихся, и у нас тоже получится плоскость (как линию нам дадут выстроенные в ряд — «параллельные» — точки). Пересекающиеся прямые дают точечную проекцию друг на друга. А параллельные лежат так плотно (фактически с нулевым расстоянием друг от друга — или, может быть, удалённые на планковскую длину), что создают плоскость, но сами не пересекаются. Когда мы подходим к плоскости, нам проще представлять что-то живое и подвижное и даже гипотетически предполагать разумное. Одномерный мультик мы не можем посмотреть: движутся отрезки, больше ничего они не могут. А в двух измерениях, в плоскости — вполне себе. Конечно, двухмерные объекты не будут проходить друг через друга насквозь, но в плоскости им есть где обходить друг друга. Например, Марио, перепрыгивающий через препятствия — это образец двухмерного мира:
Почему нам необходимо рассматривать это, когда мы говорим о времени? Потому что всеми способами, которыми жители плоского мира могут взаимодействовать с нашим миром, мы можем взаимодействовать с миром четырёхмерным. И наоборот: как четырёхмерное пространство с нами, так мы можем взаимодействовать с плоскостью.
Теперь представим такую картину. Мы плоские существа. Знаете книжку Эдвина Эбботта «Флатландия»2? Это история про плоский мир, тамошние существа в русском переводе назывались плоскатиками. Представьте, что мы — эти самые плоскатики. Мы можем друг друга обойти, мы можем друг с другом взаимодействовать по прямой, по линии: так же, как два отрезка, пересекаясь, могут «чувствовать» только точку друг друга, так два плоских существа ощущают только одну линию соприкосновения. Понятно, линия может быть и изогнутой, но это всё равно линия. Могут соприкасаться и точкой (все последующие мерности включают в себя и предыдущие). А теперь нам надо смоделировать, как мы-двухмерные будем видеть кого-то трёхмерного, и как мы-трёхмерные будем взаимодействовать с двухмерным миром, чтобы потом то же самое применить к трёх- и четырёхмерным мирам соответственно.
Представим, что все мы — плоские существа, и в нашем мире появляется некий круг:
Мы можем его осмотреть, посмотреть, насколько он ровный — идеальный круг или с искажениями, — можно определить размер и форму. Итак, мы обнаружили вот этот круг. А в другом месте мы обнаружили плоскую фигуру вот такой формы:
Мы изучили эти фигуры и делаем вывод, что это два разных объекта. Для трёхмерного человека это могут быть две руки, одна из которых просунута сквозь плоскость, а другая наложена на неё ладонью. Но для плоского человека это не заметно.
Если трёхмерный человек будет постепенно погружать руку в плоскость, то мы-плоские увидим вот такую последовательность кадров: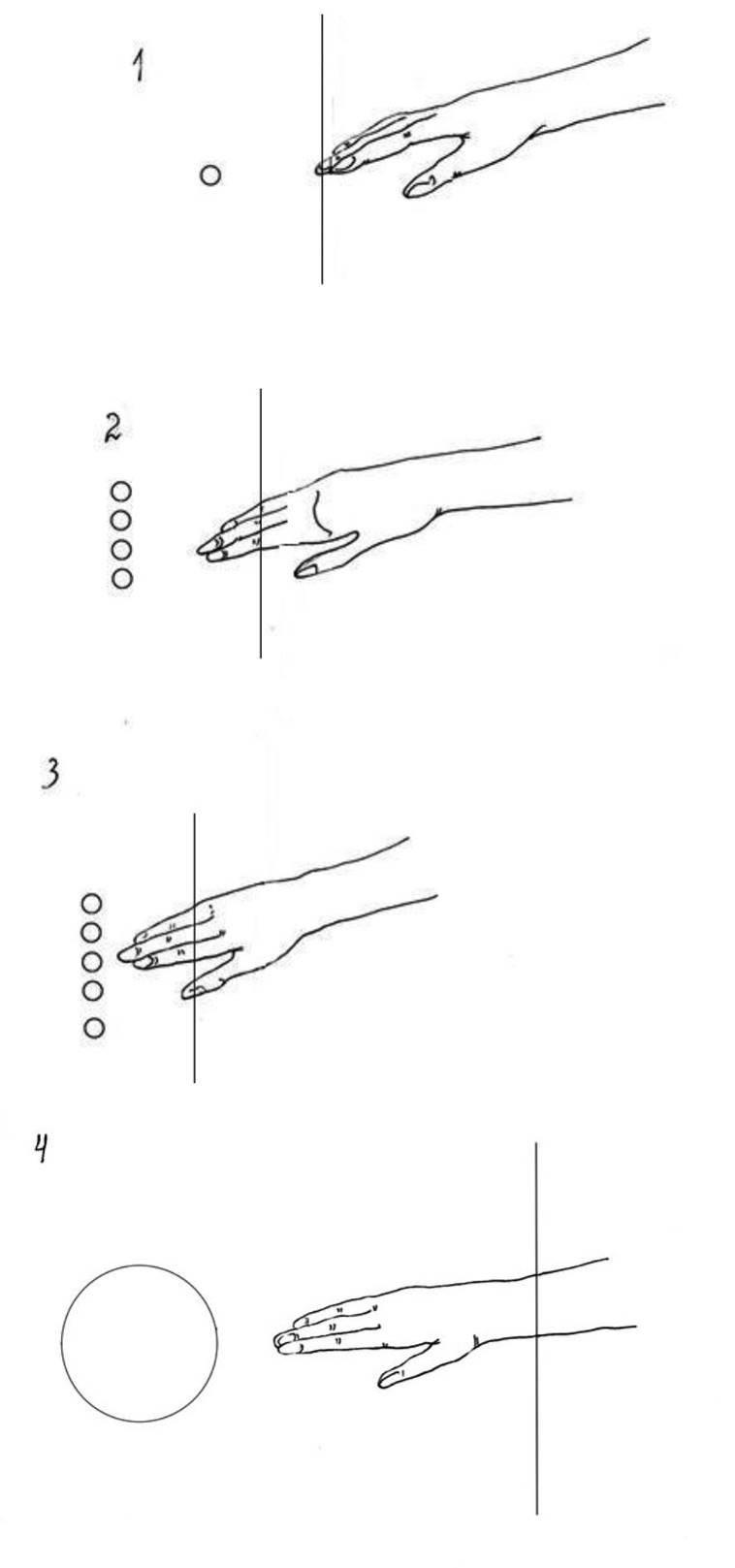
Если он будет поворачивать просунутую сквозь плоскость руку, то получим что-то в этом роде:
Если мы видим эти два объекта статично, мы не можем составить о них никакого впечатления, кроме внешнего вида. Но если мы видим динамику событий, то по этим срезам мы можем сделать вывод о том, как этот объект выглядит — если мы настолько умны, что можем задуматься о третьем измерении. Если мы видим срез за срезом, то по динамике — каждый раз зарисовывая, запоминая, анализируя, — мы можем сделать вывод, что круг и фигура с пятью выступами — это два одинаковых объекта, хотя наблюдать это непосредственно мы не можем.
Предположим, что у двухмерного пространства нас-плоских есть третье временно́е измерение, и что оно в точности соответствует третьему измерению нашего трёхмерного. Иначе говоря — что оно не перпендикулярно им всем — и нашим, и тамошним, — но и не соответствует нашему времени: что измерения могут располагаться друг относительно друга под любыми углами, а не только параллельно или перпендикулярно. Скажем, если одно измерение плоского мира совпадает с одним измерением нашего, а другое — с нашим временем, то мы такую «Флатландию» не увидим вообще, потому что в нашем мире будет только линия, а линия, как я уже говорил, нами не воспринимается. Итак, предположим, что две плоскости того мира, о котором мы сейчас говорим — это «наши» длина и ширина, а его ось времени — «наша» высота (естественно, эти понятия условны и зависят от расположения координатных осей). В нашем трёхмерном мире они располагаются ровно-ровно: два измерения совпадают, а ось времени соответствует нашей пространственной оси. И тогда для нас-трёхмерных этот плоский мир будет постоянно подниматься (или опускаться).
Вот плоскость, вот листок, вот этот мир. Вот его длина, ширина и ось времени, которая в данном случае соответствует нашей пространственной оси. Поэтому мы видим, как этот плоский мир с той или иной скоростью поднимается: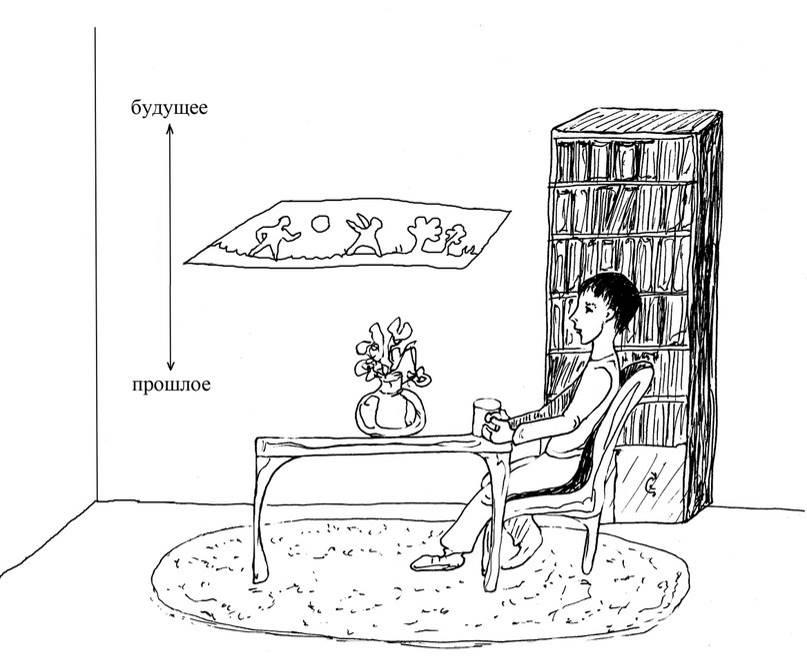
Представим, что мы поставили на его пути две руки: одну чуть ниже, другую чуть выше. Поскольку этот «лист» не имеет толщины, предположим, что он проходит наши руки насквозь. Сначала этот мир проходит одну нашу руку, получает от этого какой-то отпечаток в виде последовательных срезов, и его жители помнят, что сначала в их мире появилась такая-то фигура, потом она расширялась до такой-то, потом опять сжалась. Всё это они помнят, а потом мир начинает продвигаться через вторую руку: первая уже осталось в прошлом, а через эту наш «лист» только-только проходит. Получается, что мы держим руки одновременно, но для восприятия жителей плоского мира одну руку мы всунули в него «вчера», а другую — «завтра».
Тут мы уже подходим непосредственно к парадоксам времени. То, что с одной точки зрения произошло одновременно, с другой не является одновременным. Ещё раз напоминаю, что плоский человек не может воспринимать трёхмерный объект целиком, но если у него достаточно развитые мозги, по срезам и проекциям (особенно если видит их в динамике) он может составить представление о том, как же выглядит трёхмерный объект.
Трёхмерный мир из плоскости мы получаем точно так же, как двухмерный — из прямой: либо мы искривляем, выгибаем плоскость, либо складываем из плоскостей нечто типа стопки или книжка. Так получается трёхмерное пространство, четвёртое измерение которого тоже перпендикулярно им и образует то, что мы называем временем. Время трёхмерного мира может совпадать, а может и не совпадать со временем двухмерного, и даже время разных трёхмерных миров может не совпадать друг с другом. Для простоты я считаю, что два наших измерения совпадают с изменениями нашей «Флатландии», а их время — с третьим нашим измерением. Мы — трёхмерные, соответственно, мы можем воспринимать предыдущие измерения в их полноте (хотя не все из них можем непосредственно наблюдать; скажем, мы не можем видеть одномерное пространство). А вот о четвёртом мы можем делать выводы так же, как жители плоского мира — о нашем.
Предположим вчера рядом с нами начал появляться шарик, а потом он схлопнулся. На следующий день произошло что-то аналогичное, но чуть в стороне. Для нас это два отдельных события, которые для нас не связаны друг с другом непосредственно. Но это может это может оказаться чем-то в том же духе — скажем, что это две четырёхмерные руки, как жители плоского мира видели две наши руки. Мир сначала проходит через одну руку, затем через вторую, а потом мы перестали видеть руки вообще. Причём точно так же для четырёхмерного человека две части одного и того же объекта могли находится «на пути» нашего мира одновременно, а мы будем воспринимать это как последовательность разных событий.
«Ничто не мешает нам предположить» (как любят говорить различные альтернативные учёные, подразумевая, что у них нет доказательств), что, к примеру, этот аквариум и этот цветочный горшок — на самом деле один целый четырёхмерный объект, просто две его части, заглядывающие в наш трёхмерный мир. При этом даже не обязательно, чтобы они заметно изменялись со временем.
Вот плоский срез нашего мира; вот его ось времени:
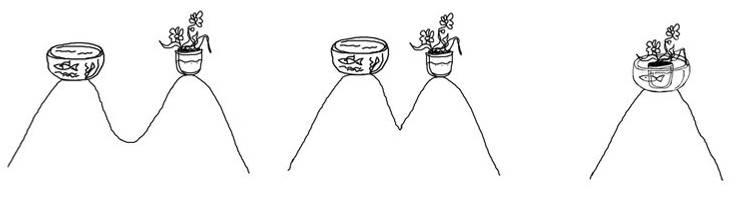
Эта плоскость поднимается через такую фигуру, одна из которых представляет собой последовательность плоских аквариумов, другая — последовательность вот этих горшков. До поры до времени (которое может исчисляться миллиардами лет) мы видим, это как два совершенно разных объекта. А потом они постепенно начинают не просто сближаться, а переплетаться между собой. Когда мир дойдёт до точки, изображённой на последнем кадре, мы увидим, что это один объект. Более того, если мы будем расширять эту модель, то мы приходим к интересному понятию как мембрана, и это может дать объяснение самым разным явлениям — от синхронии до телекинеза. Все объекты, которые мы сейчас видим — на самом деле срез, отдельные островки со своими формами. Вот этот элемент мембраны — человек, этот — стакан:
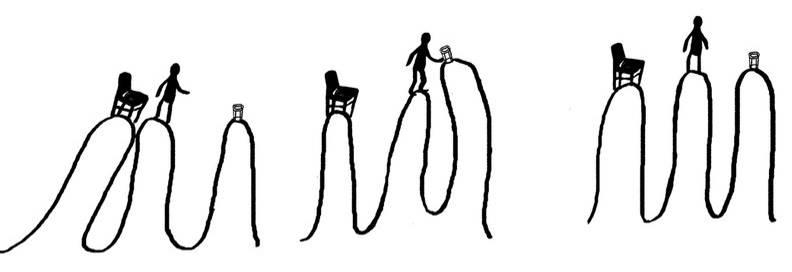
Понятно, что для нас они не кажутся соединёнными друг с другом, поскольку наше пространство — это всего лишь срез. Вот один срез, и этот срез выглядит как человечек. А этот срез выглядит как стакан. Мы можем двигаться к этому стакану. Следующий кадр — в нашей «плоскости» (в нашем трёхмерном пространстве) отсоединились эти две штучки (мембрана-человек и мембрана-стул), и кусочек под названием «человек» соединился с кусочком под названием «стакан». А потом, как нам кажется, они снова разъединились. Но их нельзя разорвать, ни одна из частей никуда не исчезает. Стакан может разбиться на осколки, может сдвинуться, а в каком-то срезе мы можем переместиться вместе с ним. Эти волны будут двигаться друг относительно друга. Но какой-то наш корень соединяет нас вместе. Мы разбили стакан, и тогда наш срез остаётся целым, а волна, которой мы обозначили стакан, теперь выглядит так, она распалась:
Если стакан расплавить, его волна смешается с какими-то другими волнами (каждый конкретный случай надо раскладывать на отдельные проекции, срезы и т. д.). И в каком-нибудь фантастическом произведении вполне допустимо представление о том, что мы соединены не через какую-то ноосферу или божество, а именно такими корешками; что фактически мы все — одно. И если мы приобретаем какую-то возможность действовать, перенося наше сознание за пределы среза нашей собственной волны, то фактически мы можем двигать этим стаканом непосредственно (то есть — осуществлять телекинез). Повторяюсь: это не попытка дать научное объяснение, а попытка создать непротиворечивую модель для фантастических произведений. Эта модель может соответствовать реальному положению дел, а может нет. Но в этой модели мы можем получать какую-то информацию (или, наоборот, воздействовать на какой-то предмет), исходя из того, что мы с ним едины.
Теперь переходим к нашему перемещению в четвёртом измерении, т. е. непосредственно к парадоксам времени. Как мы говорили о нашем воздействии на двухмерный мир, так же четырёхмерные объекты, оказываясь в нашем мире, могут создавать необычные явления. Скажем, вот появился шарик (как мы говорили, это одна из «рук» четырёхмерного существа), и мы его укололи. Через день возник ещё один шарик, мы его тоже укололи. А тот четырёхмерный человек почувствует эти два укола одновременно (если, конечно, для удобства допустить, что мы можем оказывать на него непосредственное влияние).
А отсюда уже рукой подать до того парадокса, который очень часто рассматривается в научной фантастике, когда описываются перемещения во времени. Это так называемый «парадокс бабушки». Предположим, в 2015 году нам исполнилось 25 лет, мы изобретаем машину времени и отправляемся на ней назад, скажем, на 50 лет — в том момент, когда наша бабушка должна была встретиться с нашим дедушкой. И мы (намеренно или нет) делаем что-то такое, что мешает им встретиться. Соответственно, в том варианте развития событий, который мы запустили, мы не можем родиться, а значит — не можем и вернуться на 50 лет назад, чтобы сделать то, из-за чего эта линия времени свернула в сторону: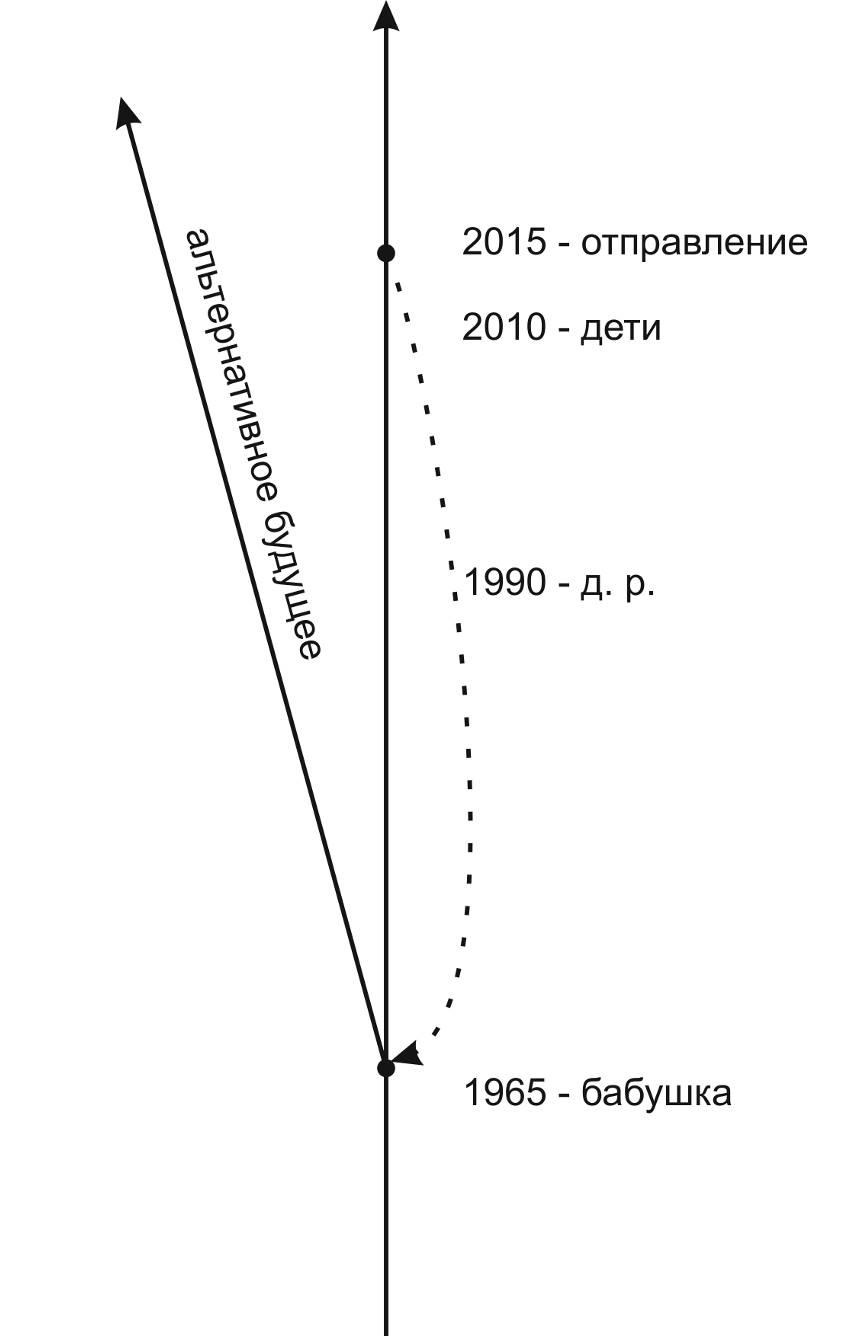
Таким образом, если мы помешали этой встрече и остались в этом времени (мы живём сейчас в ту же «сторону», куда и раньше), то мы не увидим нашего рождения. При этом если предположить, что мы «полностью и навсегда» изменили время, убрали этот вариант, выходит, что не возникло и тех обстоятельств, которые помешали этому событию. Получается очевидный парадокс: сделав что-то, мы делаем так, чтобы мы этого не сделали. Поэтому наиболее логичной в рамках «фантастической теории фантастики» вывод таков: получается, что изменение события из прошлого (как минимум, прошлого: про будущее я ещё немного поговорю дальше) ведёт к тому, что время разветвляется. У нас была наша исходная линия времени, и когда мы отправились в прошлое, она пошла уже без нас, и «нынешние» мы туда никогда больше не попадём. В исходной линии времени наши дедушка и бабушка встретились, мы родимся снова, потом снова отправимся в прошлое и там пропадём (для наших знакомых по этой ветке времени) навсегда. А мы свернули в новообразовавшуюся ветку и даже если отправимся в «своё» время (или если доживём до него), со своим «младшим двойником» мы не встретимся.
Слушатель: А если у нас там остались дети?
Fr. Nyarlathotep Otis: Если они родились до того, как мы отправились путешествовать, то они будут продолжать жить без нас. А после они, естественно, не родятся (разве что в пределах 9 месяцев), поскольку в эту ветку времени мы на машине времени вернуться уже не сможем. Скажем, я родился в 1990 году. Дожил до 2010-го, и у меня родились дети. Дожил до 2015-го, создал машину времени и отправился в прошлое. Дети продолжают свой путь и после 2015-го, но они уже знают, что папа улетел в прошлое и не вернётся. Если мы предполагаем, что линия времени единственная, что никаких разветвлений нет — то да, мы должны «исчезнуть», и детей у нас тоже не будет. Исходная линия времени идёт без нас, и мы никогда в него не вернёмся (линейными перемещениями, сонаправленными или противоположно направленными потоку времени — в прошлое или будущее). Когда мы отправились в 1965 год, мы разветвили время и теперь живём в том мире, где бабушка с дедушкой не встретились. Наши дети (если они уже родились) будут в исходной линии времени, т. е. в параллельном (или перпендикулярном, или ещё под каким-то углом находящимся) мире относительно того, где окажемся мы, переместившись на 50 лет назад. В той линии, где окажемся мы, они уже не родятся. «Второй я» в этом мире не родится тоже (его же дедушка и бабушка не встретились!), значит, он не создаст и машину времени.
Допустим, к моменту нашего отправления сюда нам 25 лет. Мы вернулись сюда за секунду нашего личного времени. А потом мы медленно и неторопливо доживаем до 2015 года (или мы садимся на машину времени и летим в будущее — но это другой разговор). Нам будет уже 75, но своих пятилетних детей мы не увидим. Мы увидим одноклассников наших детей, но без них самих, или наших одноклассников, которые нас не знают, потому что они родились, а мы в этой линии никогда не рождались, мы только дожили до этого времени из 1965 года. Мы переместились в совершенно новый мир, и вернуться в наш исходный мы можем только непосредственно через пятое измерение, а не по линиям четвёртого измерения — прошлое-будущее (но об этом чуть позже). А там, где мы оказались, будет точно такой же мир, как тот, который мы покинули, отправившись в прошлое, но конкретно новых нас и вообще всего того, что натворили наши бабушки, дедушки, папы, мамы и мы сами, — этого всего не будет. И, соответственно, не будет наших детей. Мы не застанем здесь рождения самих себя. А вот если бы нам удалось попасть в исходную ветку — было бы интереснее. Потому что тут мы как раз родились бы.
Теперь насчёт скорости течения времени. Здесь тоже начинаются интересные парадоксы. Будут ли эти 50 лет, которые прошли между моментом встречи бабушки с дедушкой и нашей отправкой в прошлое, теми же 50 годами для этой жизни? Естественно, какие-то 50 лет пройдут: понятно, что когда мы живём внутри нового потока времени, мы точно так же проживаем 50 кругов «местной» Земли вокруг «местного» Солнца. Но интересный момент: мы не знаем, идёт ли новая ветка времени строго параллельно старой или же под каким-то углом у ней. Если они строго параллельны, то всё понятно, они идентичны по скорости, просто дальше начинаются расхождения по событиям: мы не родились, мы не сделали то-то и то-то и т. д.: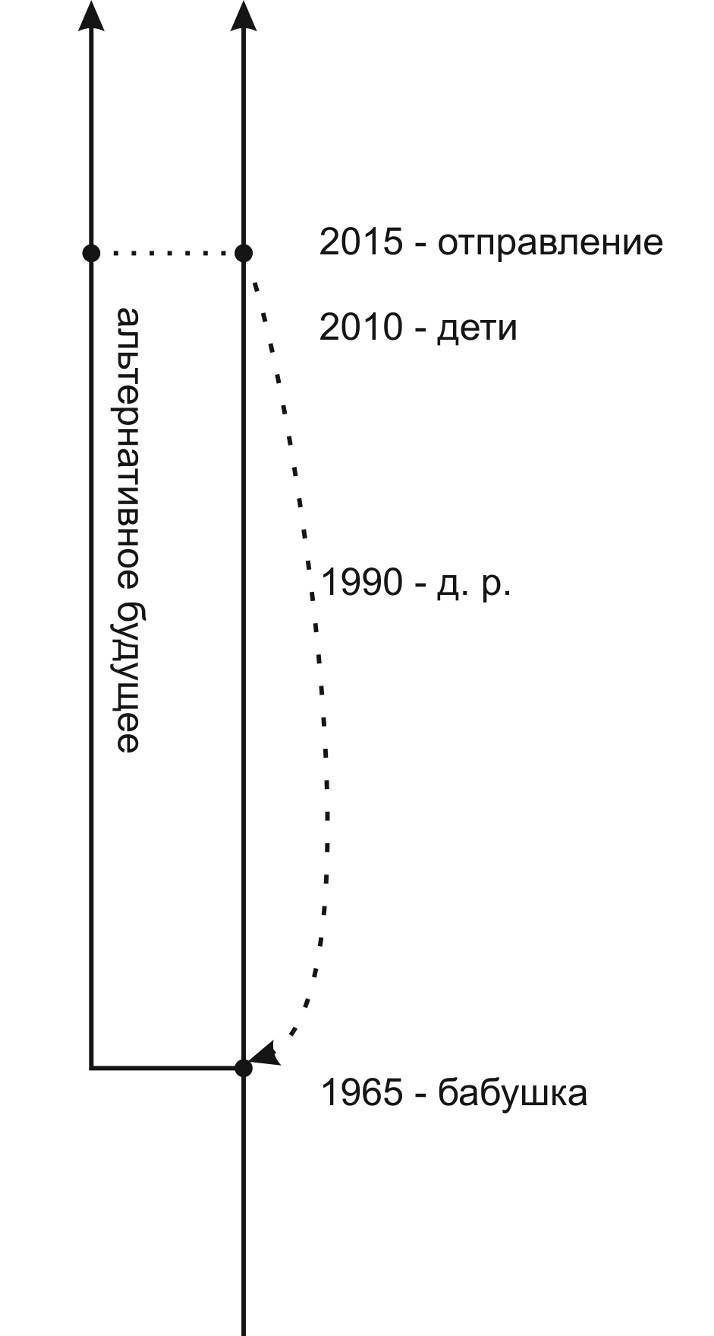
Если в варианте, где они строго параллельны, мы выстраиваем мостик между ними через пятое измерение, то, прожив эти 50 лет, мы перейдём, скажем, из 10 декабря 2014 года новой ветки в 10 декабря 2014 года исходной ветки. И там прошло 50 лет, и тут прошло 50 лет. А вот если время движется не строго параллельно, а под углом, ситуация будет совсем другая. Ситуация будет напоминать парадокс близнецов, который, наверное, более известен. Суть в том, что в этом случае мы можем выстраивать перпендикулярный вектор двумя способами: либо перпендикулярный исходному времени, либо перпендикулярный новосозданному времени. И если мы пытаемся переместиться между параллельными мирами, то в зависимости от того, каким именно способом выстраивается этот перпендикуляр (перпендикулярно исходному времени или перпендикулярно времени, куда мы возвращаемся), мы будет оказываться в разных временах, которые вычисляются геометрически, по теореме Пифагора. Если мы, прожив 50 лет и затем двигаясь непосредственно через пятое измерение, отправимся перпендикулярно исходному времени, мы попадём не в 2015 год, а, скажем, на 5 лет раньше и увидим рождение своих детей и то, как мы строим машину времени, а в 2015 году окажемся не через 50, а через 55 лет после 1965 года. Но если мы перемещаемся перпендикулярно новосозданному времени, то через те же 50 лет нашего субъективного времени мы окажемся в 2020 году нашего исходного мира (при условии, конечно, что движение между ветками осуществляется мгновенно или практически мгновенно по нашему субъективному времени — как раньше мы допускали это для перемещения на машине времени):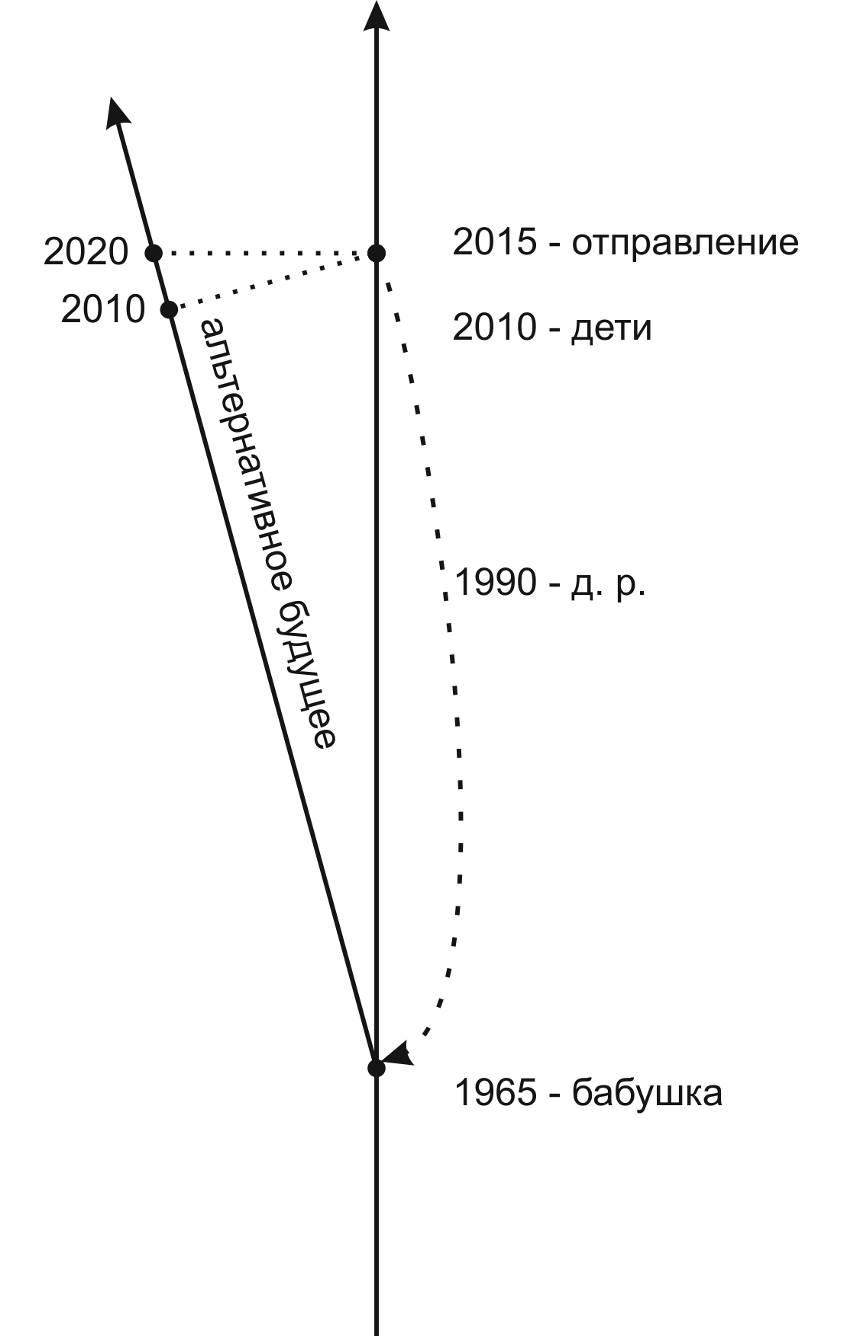
Если кто не помнит, парадокс близнецов обычно касается приближения к скорости света. Но то же самое мы можем проследить и здесь. Предположим, у нас есть близнец. Он находится в исходном мире, когда мы из него уже исчезли. Если мы отправились в прошлое, помешали встрече бабушки и дедушки и сразу же вернулись в 2015 год, а затем, двигаясь через пятое измерение под равными углами к исходному и новому миру, вернулись в исходный мир, ему будет 25, а нам незначительно больше. Если мы выстраиваем перпендикуляр исходному миру, то к моменту нашей встречи нам будет 25, а ему 20. Если перпендикулярно нашему новому миру — то нам будет 25, а ему 30. А вот если мы не пользуемся машиной времени для возвращения в 2015 год, а потом переходим в исходную ветку через пятое измерение — то нам будет 75 лет, а ему в первом случае те же 25, во втором — 20, в третьем — 30.
Раз уж мы заговорили о парадоксе близнецов, то теперь перейдём к вопросу путешествия в будущее. Самый интересный момент — что оно осуществимо. Во всяком случае, отправить послание в будущее вполне реально: надо просто разогнать его до скоростей, близких к скорости света. Понятно, что с человеком это не пройдёт. Но предположим (поскольку сейчас мы говорим не о физике, а о фантастике), что создали устройства, которые сохраняют стабильную среду в нашем космическом корабле, движущимся со скоростью, близкой к скорости света. Тогда наше путешествие в космическом корабле будет, фактически, путешествием в будущее. Конечно, это будет будущее без нас, без нашего присутствия, а не так, что мы решили отправиться в будущее и посмотреть, что с нами случится через 20 лет. Через 20 лет будут всего лишь помнить, что мы улетели 20 лет назад. Путешествие в будущее, в отличие от путешествия в прошлое, достаточно легко осуществимо (теоретически, конечно) и при этом не вызывает парадоксов. Сами с собой мы в этом случае не встретимся, мы не сделаем ничего такого, что изменит нашу дальнейшую жизнь. Наша линия, если мы путешествуем в будущее, достаточно проста: раз — мы уже здесь и живём дальше. Она непрерывна и направлена в одну и ту же сторону.
Теперь продолжим о многомерном пространстве. В той модели, которую мы рассматриваем, время — четвёртое измерение. Вспоминаем, что мы говорили об измерениях более низкого порядка — скажем, о линии. Когда мы разветвляем прямую (первое измерение), мы задаём плоскость (второе измерение), между частями которой уже могут быть какие-то взаимодействия. Мы говорили, что практически невозможно представить обитателей первого измерения, а обитателей второго — уже достаточно легко. Если пространство одномерное — линия, — то все взаимодействия — только в этой прямой, а если мы его разветвили — возможны переходы между ветками. Разветвляя время (четвёртое измерение), мы подходим к пятому измерению. Плоскость на той проекции, которую мы нарисовали — та самая, где лежит наше дерево «альтернативных историй» — это и есть пятое измерение. Если у нас имеется такое дерево с разной скоростью течения времени внутри веток (потому что они могут отходить от изначального ствола под разными углами), все они вместе находятся в пятимерном пространстве. Мы уже немного говорили о мостиках между этими ветками, о «параллельных» (или каких-то ещё) мирах, чуть позже поговорим о них дальше. Не знаю, можно ли называть эти мостики «червоточинами», поскольку «червоточины» — это нечто в пределах одного пространства. Но до этого мы сейчас дойдём.
Тут уже для фантастики огромный простор. Некий исходный мир от момента Большого взрыва до какой-нибудь кварковой, или инфляционной, или планковской эпохи. Или мы можем взять вариант от возникновения Брахмы до первого его дня. Исходная концепция может быть физической, может быть мифологической и какой угодно ещё. В общем, от возникновения или сотворения мира до первого разветвления времён. По каким причинам они разветвляются — это уже отдельный вопрос. Может быть, они разветвляются постоянно, всё множество вариантов, которые вообще возможно. Допустим, есть мир, где я поднимаю руку, есть мир, где я опускаю руку и т. д. Читали, наверное, «Хроники Амбера» Желязны? Там как раз это описывается. У него такая концепция, что всё, что только можно представить, существует в одном из таких параллельных миров (там они называются Отражениями). Где-то есть мир, где, скажем, этот листок лежит справа от ручки, где-то — слева. В книге «Автостопом по галактике» рассматривалась схожая концепция, но там исходили не из модели Мультивселенной, а из того, что сама наша Вселенная бесконечна, и поэтому наверняка любой предмет, который можно вообразить, может оказаться в одной из «далёких-далёких галактик».
Не забываем при этом, что временные измерения — это не какие-то отдельные от пространственных. Может быть трёхмерный мир с четвёртым измерением в качестве времени, похожий на наш, но его время может располагаться перпендикулярно нашему: два измерения могут совпадать, а его четвёртое может идти в одном из наших пространственных. Тогда мы можем увидеть его прошлое и будущее как наше обычное пространство, но не можем увидеть одно из его пространственных измерений. Его обитатели для нас будут фактически тем, чем мы являемся для четырёхмерного человека, — а мы являемся… длинными-длинными извивающимися червячками, которые начинаются в животе у другого такого же червячка, а потом увеличиваются, перемещаются, многократно пересекают свой собственный след и т. д. Если мир у такого существа трёхмерный, но расположен перпендикулярно нашему (т. е. ось времени совпадает не с нашей осью времени, а с одной из наших пространственных), мы будем видеть как раз этого «червячка», состоящего из его возрастных срезов. Мы не будем видеть его объёма, но в качестве объёма мы будем видеть его эволюцию во времени:
Поехали дальше. Вот у нас образовалось дерево «альтернативных историй». Если веточка отделилась недалеко, то мир, который там — это фактически тот же самый мир, но где действительно чехол от мобильника лежит чуть иначе. Отличия будут минимальны. Грубо говоря, если мы случайным образом попали в недавно отпочковавшийся мир, мы можем даже не заметить этого. Какие-то изменения могут быть, но не попадаться нам на глаза, или мы на них не обратим внимания. Но может быть интереснее. Я думаю, что у вас такое могло бывать в жизни, что всё как обычно, но я точно был уверен, что вон та вывеска была зелёная, а сейчас она красная, хотя никто её не менял. Когда воспринимается, что оно было другим. Это может объясняться парамнезией (ложной памятью) в рамках психологии или физики. Но, если мы говорим о фантастике, то, попадая в такие недавно отпочковавшиеся миры, мы можем не узнать, что оказались в этом мире, но нам постоянно будут попадаться такие обескураживающие детали. Такой эффект бывает, когда человек очень сильно думает о чём-то — допустим, что он был в Бразилии, видел джунгли, зелёный цвет. Потом он посмотрел на вывеску, накладывая зелёный цвет, а она на самом деле красная. Психологических объяснений может быть много. Я не говорю, что верна именно моя, я говорю, как эти представления о многомерном мире можно использовать в фантастике. Я не пытаюсь доказывать существование чего-то сверхъестественного.
Почему я говорю, что концепция такого дерева даёт огромное многообразие для сотворения фантастических миров? Если мир отделился давно, век назад, то может оказаться, что здесь не Калининград, а Кёнигсберг. Чем раньше произошло отделение мира, тем больше будут отличия. Соответственно, если мы попадаем в очень-очень-очень давно отделившиеся миры, то там могут быть отличия даже на уровне физики. Грубо говоря, те события, которые произошли в момент Большого взрыва: какие-то базовые величины установились каким-то другим образом — и всё будет по-другому.
Теперь представим себя пятимерными путешественниками по пятимерному пространству. Но для начала представьте себя трёхмерных в такой ситуации. Вы находитесь в лесу, и вам надо найти «цивилизацию»: посёлок, станцию, дорогу и т. д. Вы оглядываетесь по сторонам, слушаете, нет ли звука проезжающего поезда, нет ли просвета, — в общем, ориентируетесь своими трёхмерными чувствами и выискиваете признаки нужного вам объекта. А теперь мы — пятимерные путешественники по пятимерному пространству, наше собственное время — это шестое измерение. Что мы будем видеть? Мы видим здесь наш мир, а чуть рядышком своими пятимерными чувствами видим мир, в котором есть небольшие отличия. Здесь мобильник по-другому лежит. Мы смотрим дальше и примерно прикидываем, в какую сторону нам двигаться, чтобы дойти до мира, который нам нужен. Опять же: концепция путешествия по Отражениям, которая описана у Желязны, будет практически осуществима для пятимерного существа. Нам надо, чтобы на этом месте оказался океан. Мы смотрим по сторонам — так же, как в трёхмерном мире. Ага, скорее всего, вариант развития мира, где здесь океан, находится в той стороне. Пошёл. Упс, немножко не туда! Повернул.
Попробуем с более простой ситуацией, когда на полу валяется кошелёк полный денег. Нам нужно сейчас кошелёк, полный денег. Нам не надо заходить в давно отделившиеся миры, мы оглядываем соседние. Потому что наверняка по теории вероятности, если мы осмотрим достаточно большое количество миров, то кто-нибудь здесь забудет свой бумажник.
Слушатель: А где взять время на этот осмотр?
Fr. Nyarlathotep Otis: Время у нас перпендикулярно. Оно ограничено нашей продолжительностью жизни в шестом измерении.
Давайте спроецируем пятое измерение на второе: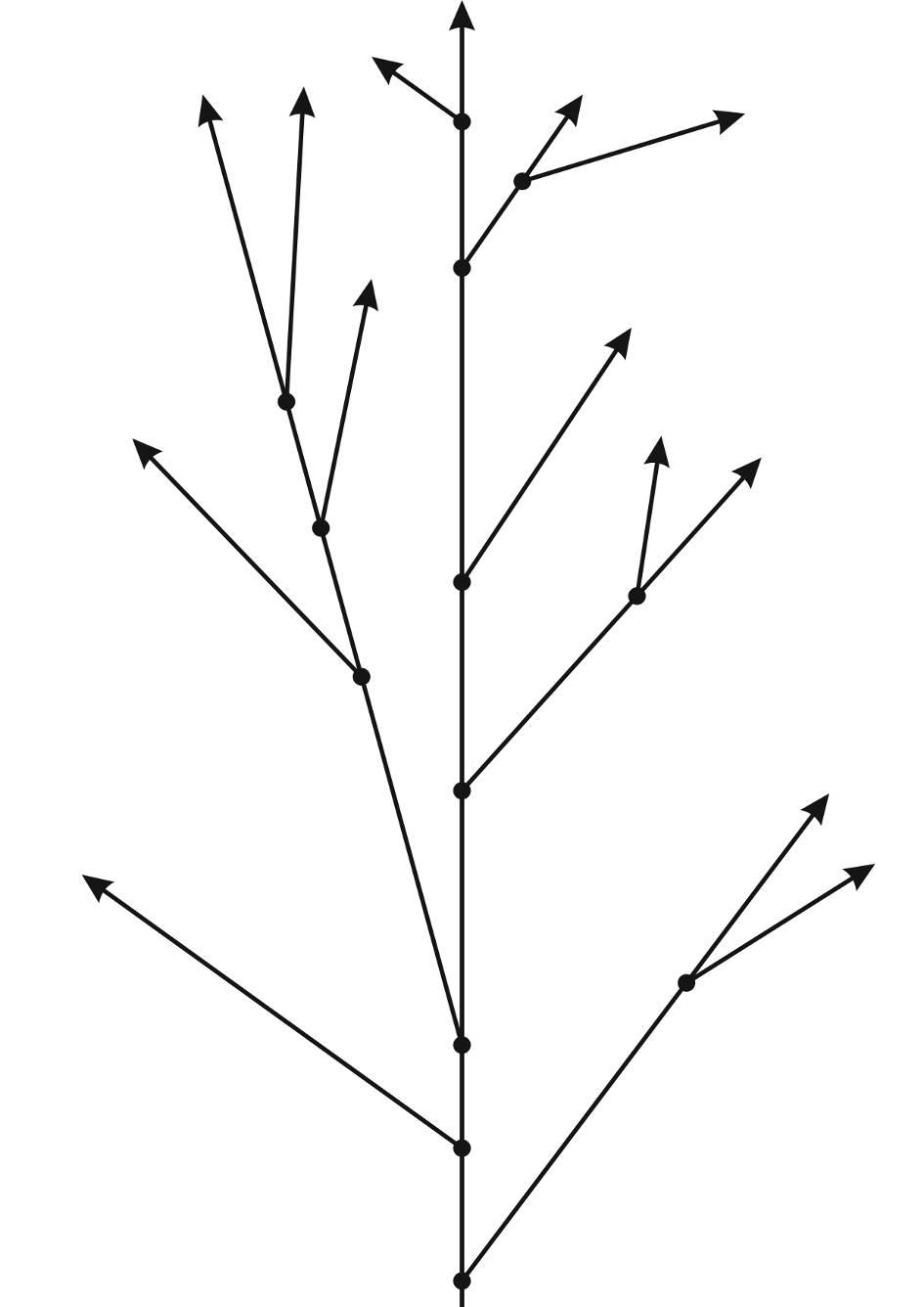
Вот это дерево — наше пятимерное пространство. Мы спроецировали его на этот лист, т. е. на плоскость. Мы сами тоже пятимерные и бродим вот здесь свободно. Мы можем зайти в это прошлое, можем зайти в это будущее и т. д. Наше личное время тоже, естественно, тикает, но оно тикает перпендикулярно. Мы стареем, но при этом мы смотрим на это дерево в статическом расположении. Мы гуляем по этому дереву, и если будем топать в далёкое прошлое, то это будет дольше, или мы можем воспользоваться какой-то машиной. Пока мы бродим где-то, где можно найти этот бумажник, мы бродим в соседних мирах (то есть это соседние миры для трёхмерных существ, а для пятимерных это фактически один мир).
Ещё раз: трёхмерное пространство — это наш мир. У него есть четвёртое измерение, которое воспринимается нами как время. Вспоминаем: плоскость движется в нашем третьем измерении. Наше третье измерение обитателями этой плоскости не воспринимается как пространство, но мы видим эту плоскость поднимающейся сквозь наше трёхмерное пространство. То же самое и наш трёхмерный мир. Он поднимается от прошлого к будущему, и, соответственно, в нём при этом движении происходят изменения. Но сами мы не видим четвёртое измерение непосредственно. То же самое касается и разветвления.
Представление о пятом измерении берётся из разветвления времени, т. е. из этих парадоксов, когда мы изменяем направление времени. Каждое такое изменение создаёт дополнительную веточку, и все эти веточки лежат в своей «плоскости» — в пятимерном пространстве. Если мы трёхмерные — мы этого не видим, если четырёхмерные — мы можем свободно двигаться по тому, что трёхмерные существа воспринимают как направления времени, и по развилкам, возникающим при отпочковывании новых веток времени, переходить из одной такой ветки в другую. Когда мы переходим из мира, где мобильник лежит с правой стороны стола, в мир, где он лежит с левой стороны стола, для нас это будет выглядеть как плавно перемещающийся справа налево мобильник. Будут происходить те же изменения, какие у нас происходят во времени, но происходить они будут другим образом — как будто это мы меняем своё местоположение. И если мы смотрим за падающим и разбивающимся стаканом, то мы можем проследить, как разлетаются его осколки, а потом вернуться к той точке, где стакан снова целый, и так делать сколько угодно раз. Это что касается четырёхмерного существа, перемещающегося в пятом измерении (как мы-трёхмерные можем ходить по поверхности земли). А пятимерный человек в таком пятимерном пространстве свободно перемещается и в прошлое, и в будущее, и в параллельно существующие ветви. У него есть своя ось времени — то, что для него время.
Конечно, какая из осей является временем, тоже относительно. Но ведь и про пространственные измерения мы не можем сказать, куда именно направлены эти три оси. Мы можем положить мобильник, и тогда его высота будет сантиметр, а длина — 20 сантиметров, но мы можем его поставить, и тогда всё будет наоборот. Так же и время может располагаться перпендикулярно. Наше время, параллельное время, перпендикулярное время… Если мы живём в перпендикулярном времени, то мы будем жить через срез параллельных времён. У них не будет прошлого в нашем понимании, но мы будем проживать всю последовательность изменений как миры с мобильником, расположенным так, так и так. Мы будем проживать всё это, и мобильник для нас будет двигаться (если мы трёхмерные, и наша ось времени совпадает с этой осью времени). Все эти оси — очень условно, направление времени может идти и под любым другим углом, и тогда некоторые изменения будут временными, а некоторые — связанными с параллельными мирами. Но я беру самые простые случаи, где всё строго перпендикулярно. В общем, до шестого измерения мы доходим достаточно легко, это всего лишь «время» для пятимерных существ, свободно перемещающихся из одной вероятностной ветки в другую не только по «тоннелям» времени, но и между ними, независимо от угла и направления ответвления. А седьмое измерение… Это уже дебри, их надо осмысливать, и осмысливать их надо с геометрией. Пока мы не поймём, через сколько точек какие пространства строятся, как вычисляются углы между ветками и пр. — идти дальше не имеет смысла.
Теперь к многомерности и к возникновению Вселенной. Есть всякие теории, связанные с суперструнами, супергравитацией, с мембранами… Вот Вселенной нет, затем возникает точка, и Вселенная начинает расширяться. Как это может выглядеть в измерении на порядок больше?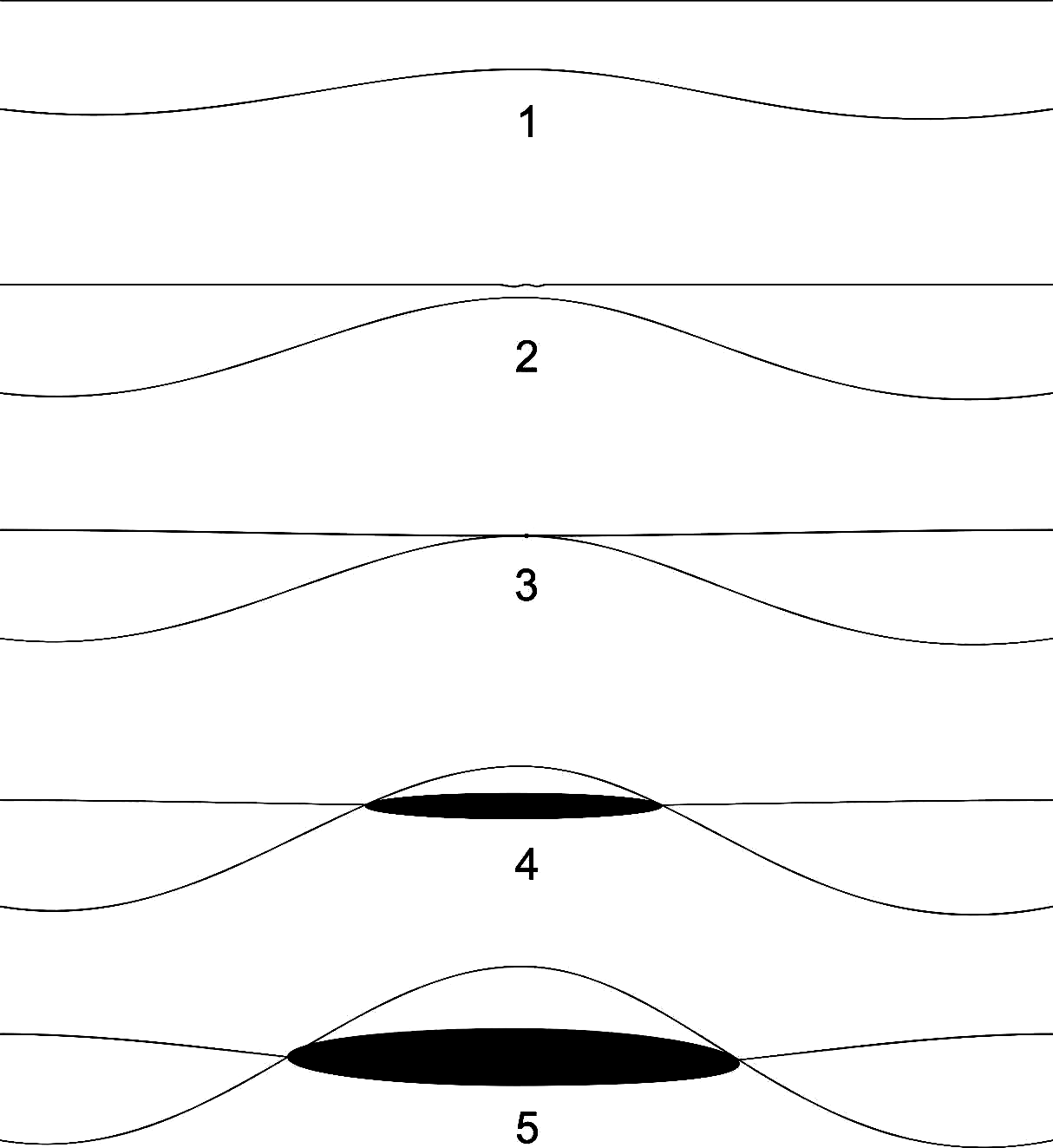
Вот две мембраны высокой размерности, превосходящей нашу. На первом кадре один изгибается в сторону другой. Здесь он совсем не касается второго мира. На втором — тоже не касается, но уже приблизился и может вызвать гравитационное или какое-то ещё искажение. На третьем миры-мембраны соприкоснулись. И на их пересечении появляется точка. Нашего мира ещё нет, потому что наш мир и есть взаимодействие. Сперва нашего мира здесь нет, дальше наш мир выглядит как точка соприкосновения двух мембран — это и есть момент Большого взрыва. А на последних кадрах наш мир пошёл расширяться (поскольку «площадь», «глубина» взаимодействия двух мембран возрастает).
Эта теория многое объясняет. В частности, объясняет, почему гравитация является самым слабым видом взаимодействия. Конечно, с точки зрения обыденного восприятия, она кажется самой сильной. Но представьте маленький магнит и маленькую иголочку. Вы подносите магнит — и иголка притянулась. А что гравитация? Можно ли гравитацией притянуть аналогичный объект с помощью чего-то столь же маленького? Конечно, мы можем вспомнить про вихри, смерчи и много про что ещё. Это очень мощные явления, но ведь размер магнита и размер Земли всё-таки немного разный. Гравитация действует только в том случае, если есть очень массивный объект, а электромагнитное может проявиться и от гораздо меньшего объекта. Можно сколько угодно говорить, что мы держимся на Земле за счёт гравитации, но с физической точки зрения сила гравитационного взаимодействия исчезающе мала по сравнению со всеми остальными взаимодействиями. Для того чтобы объяснить, где прячется остальная часть этой гравитации, учёными как раз вводится представление о мембранной вселенной. Существуют много мембранок, и многие из них в разные моменты своего личного времени могут соединяться и давать эту самую точку, которая расширяется, создавая эффект Большого взрыва. И как раз в данном случае я говорю не столько о фантастике (потому что в фантастике это не применить), сколько о современных физических представлениях. Подробнее об этом вы можете узнать в фильме BBC «Параллельные вселенные», текст из которого я привожу ниже.
1 Транскрипт составил Нёманскі Вір, ред. Fr. Nyarlathotep Otis.
Схемы и иллюстрации — Fr. Nyarlathotep Otis, Наталия Гиндикина, а также из сети Интернет.